机器学习中的函数总结 2019-03-09

机器学习中的函数总结

在机器学习中经常会遇到很多函数的概念。这些函数概念非常重要！但在一开始的时候，经常容易混淆这些这些函数概念，这里集中进行了一下概述，方便区分和加强印象。

常见函数概念

假设函数(hypothesis function, hypothesis )

对样本的假设模型函数，根据先验知识做的模型预测。[1]

常用假设函数有：

线性函数：线性回归

f(x) = w^Tx + b

sigmoid函数：逻辑回归

f(x) = \frac {1}{1+e^{-x}}

通常损失函数为交叉熵

softmax函数：多分类问题

f\,(\bold{z}) = \frac {e^{z_i}}{\sum_{j=1}^{K}e^{z_j}}, \enspace for \enspace i=1,...,K\, and \enspace \bold{z}=(z_1,...,z_K) \in R^K

通常损失函数为交叉熵分类损失函数：

Loss_i = -\sum_i{y_i}\log{y'_i}

损失函数(lost function, error function)

参考：https://www.zhihu.com/question/52398145

单个训练样本上的

| y_i - f(x_i)|

常用的有[3]：

均方误差损失函数(Mean Squared Error, MSE)：

Loss = \frac 1 2 (y_i-y_i')^2

交叉熵、对数损失函数:

https://en.wikipedia.org/wiki/Cross_entropy

\begin{aligned} Loss\,(Y, P(Y|X)) &= -\log{P(Y|X)} \\&=-[y\log(y') + (1-y)\log(1-y')] \\&=log(1+e^{-yy'}) \end{aligned}

常用于与逻辑回归

平方损失函数、最小二乘法(Oridinary Least Squares, OLS)

Loss\,(y, y') = (y-y')^2

指数损失函数：

Loss\,(y, y') = \exp(-yy')

用于：adaboost

合页损失函数(hinge)：

https://en.wikipedia.org/wiki/Hinge_loss (from: https://www.zhihu.com/question/47746939)

Loss\,(y, y') = \max (0, 1-y \bullet y')

用于：svm

0-1损失函数

Loss\,(y, y')= \begin{cases} 0 &\text{ if } sign(y) \neq sign(y') \\ 1 &\text{ if } sign(y) = sign(y') \end{cases}

绝对值损失函数

Loss\,(y, y') = |y-y'|

代价函数、成本函数(cost function)

整个训练集上面的

\frac{1}{N} \sum_{i=1}^N|y_i-f(x_i)|

目标函数(object function)

\min \frac{1}{N} \sum_{i=1}^N|y_i - f(x_i)| + \lambda J(f)

J:正则项，一般使用L1或L2正则化

激励函数、激活函数(activation function)

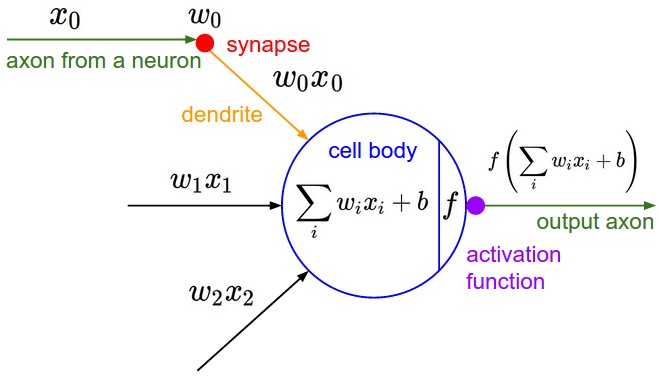a neuron (from: http://cs231n.github.io/neural-networks-1/)

扭曲翻转特征空间，寻找线性边界。[6] 常用的有

sigmoid：

f\,(x) = \frac {1} {1 + e^{-x}}

tanh(双曲正切函数)：

f\,(x) = \frac {\sinh(x)}{\cosh(x)} = \frac {e^x-e^{-x}}{e^x+e^{-x}}

ReLU(Rectified Linear Unit, ReLU, 线性整流函数，修正线性函数)：

f\,(x) = x^+ = \max(0, x)

softmax:

f\,(\bold{z}) = \frac {e^{z_i}}{\sum_{j=1}^{K}e^{z_j}}, \enspace for \enspace i=1,...,K\, and \enspace \bold{z}=(z_1,...,z_K) \in R^K

总结

假设函数h(x):假设样本与目标的拟合函数

损失函数L(x):评价样本与预测值的单个误差函数

代价函数J(x):平均样本与预测值的整体误差函数，也就是经验风险函数

目标函数J(x):整体结构风险，相比于经验风险多出了正则化项

激活函数a(x)：神经元对结果的非线性化处理。类似于假设函数，但只针对单个神经元。

参考

[1] https://stanford.edu/~shervine/teaching/cs-229/cheatsheet-supervised-learning#notations

[2] https://www.zhihu.com/question/52398145

[3] http://www.csuldw.com/2016/03/26/2016-03-26-loss-function/

[4] https://en.wikipedia.org/wiki/Cross_entropy

[5] https://www.zhihu.com/question/47746939

[6] https://www.zhihu.com/question/22334626

[7] http://cs231n.github.io/neural-networks-1/

[8] https://blog.csdn.net/google19890102/article/details/50522945